PODLIST

Oszillationen

Download

Diese Folge entstand im Rahmen eines Projekts zur Modellbildungsvorlesung von Gudrun. Es ist eine Arbeit von Yannik Brenner, Bastian Hasenclever und Urs Malottke, die das Ziel haben, in einigen Jahren Mathematik und Physik am Gymnasium zu unterrichten. Außerdem macht Yannik selbst Musik und hat sich deshalb ganz praktisch mit Schwingungen an der Gitarre beschäftigt. Die drei hatten die Idee, dass man das Thema Schwingunge interessant für die Schule aufbereiten kann, wenn es dazu auch Hörbeispiele gibt. Deshalb haben Sie sich an einen Tisch gesetzt, das Gespräch und die Hörbeispiele aufgenommen und schließlich den Text dazu aufgeschrieben.

Der harmonische Oszillator spielt eine wichtige Rolle zur Modellierung verschiedenster physikalischer Sachverhalte. Daher bietet es sich an, ihn schon in der Schule zu thematisieren, wo er auch in der Oberstufe im Bildungsplan zu finden ist. Während im Podcast der Versuch unternommen wurde, ein Grundverständnis für das Thema ohne formale Zusammenhänge zu entwickeln, sollen hier zusätzlich die mathematischen Hintergründe gemeinsam mit einigen Abbildungen ergänzt werden. Die didaktischen Aspekte, die in der Episode zur Sprache kommen, spielen im folgenden Text jedoch nur eine untergeordnete Rolle.

Grundlegendes


Ein Oszillator ist ein System, das um einen bestimmten Punkt, in der Regel Ruhepunkt oder auch die Ruhelage genannt, schwingen kann. Befindet sich das System in Ruhe in dieser Ruhelage, passiert ohne die Einwirkung äußerer Kräfte nichts; wird das System von diesem Punkt ausgelenkt, wird es durch eine rückstellende Kraft wieder Richtung Ruhepunkt beschleunigt. Der Zusatz "harmonisch" bedeutet, dass die Rückstellkraft linear von der Auslenkung zum Ruhepunkt abhängt, also proportional zur Auslenkung zunimmt. Der Graph der Bewegungsfunktion ist eine Sinus- oder Cosinus-Kurve.
Die einfachsten und wohl auch bekanntesten Beispiele eines Oszillators im Bereich der Mechanik sind das Faden- und das Federpendel. Beim Fadenpendel ist der niedrigste Punkt die Ruhelage und die Rückstellkraft resultiert aus der Gravitationskraft. Beim Federpendel stellt die Federkraft die rückstellende Kraft dar.

Eigenschaften eines harmonischen Oszillators

Ein schwingfähiges System besitzt verschiedene Eigenschaften, mit deren Hilfe das gesamte System beschrieben werden kann. Um den harmonischen Oszillator zu verstehen, kann man sich zuerst die Bewegungsgleichung ansehen, also die Gleichung, die die aktuelle Lage des Systems beschreibt. Ausgangspunkt ist die Rückstellkraft, die im mechanischen Fall linear von der Auslenkung zur Ruhelage, also dem aktuellen Ort, abhängt (auf nicht-mechanische Einsatzgebiete wird später eingegangen). Die Rückstellkraft F kann mit einer Variablen k, die von verschiedenen Merkmalen des Systems abhängt, gemeinsam mit dem Ort also als

$F(t) = -k\,x(t)$

dargestellt werden. Die Kraft kann auch als Beschleunigung a, also der zweifachen Ableitung des Ortes, mal der Masse m ausgedrückt werden, wodurch die Formel auch folgendermaßen aussehen kann:

$ F(t) = m\,a(t) = m\,x''(t) = -k\,x(t) \quad\Leftrightarrow \quad m\,x''(t) + k\,x(t) =0 \quad \Leftrightarrow \quad x‘‘(t) + k/m\,x(t) = 0 $

Diese Art von Formeln, in der eine Größe gemeinsam mit einer ihrer Ableitungen auftritt, wird Differentialgleichung genannt.
Das Erarbeiten einer Lösung ist leichter, wenn durch \omega_0^2 = k/m die Gleichung vereinfacht wird. \omega_0 wird die Eigenfrequenz des Systems genannt und gibt außerdem an, wie viele Schwingungen das System in einer bestimmten Zeit, oftmals einer Sekunde, macht, wenn keine anderen Kräfte vorliegen. Somit ergibt sich

x''(t) + \omega_0^2\,x(t) = 0\,.

Die Lösung der Funktion für den Ort x(t) muss eine Funktion sein, die nach zweimaligem Ableiten bis auf einen Vorfaktor und das Vorzeichen wieder die Ursprungsfunktion ist. Deshalb sind Sinus- und Cosinus-Funktionen, oder die äquivalente Darstellung durch die e-Funktion (siehe Eulersche Formel), Lösungen. Werden nun

$ x_1(t)=A\sin(\omega_0 t), \qquad x_2(t)=B\cos(\omega_0 t)$

gewählt, wobei A und B die Amplituden, also maximalen Auslenkungen der Schwingungen darstellen, kann mit den Ableitungsregeln überprüft werden, dass dies Lösungen für die Bewegungsgleichung sind.

Als Summe zweier Lösungen ist auch

$ x(t):= x_1(t)+x_2(t) = A\sin(\omega_0\,t)+B\cos(\omega_0\,t)\,. $

Eine Lösung, die die allgemeine Lösung genannt wird. Die beiden Amplituden der einzelnen Sinus-/Kosinus-Funktion müssen dabei aus Anfangsbedingungen bestimmt werden. Man sieht, dass B die Amplitude der beobachtbaren Schwingung sein muss, also der maximalen Auslenkung, die beim Zeitpunkt t=0 vorliegt, da die Gesamtschwingung zum Zeitpunkt t=0 diese Auslenkung annehmen muss und zu diesem Zeitpunkt der Sinus verschwindet:

$ B=x(t=0)=x_2(t=0) \,.$

Die Amplitude der Sinus-Funktion bestimmt sich nach

$ A=1/\omega_0 \,x’(t=0) $

und spielt daher dann eine Rolle, wenn zum Zeitpunkt t=0 bereits eine Geschwindigkeit vorliegt, das System also nicht aus der Ruhe losgelassen, sondern angestoßen wird.

Zu besprechen ist allerdings noch, wie die Gleichung bei einem anderen Pendel als dem Federpendel aussieht. Das Prinzip des Oszillators bleibt gleich und somit natürlich auch die Mathematik, die ihn beschreibt. Allerdings setzt sich \omega_0 bei anderen Pendeln anders zusammen, da bei ihnen andere Rückstellkräfte und andere Systemeigenschaften eine Rolle spielen und nicht die Federkonstante und Masse wie beim Federpendel. So gilt beim Fadenpendel

$\omega_0^2 = g/(2l\pi) \,,$

wobei g die klassische Gravitationskonstante ist, die beim Fadenpendel eine große Rolle für die Rückstellkraft einnimmt, und l die Fadenlänge darstellt. Werden Oszillatoren außerhalb der Mechanik betrachtet, beispielsweise der elektrische Schwingkreis, ergibt sich \omega_0 aus den Eigenschaften, die dieses System beschreiben. Beim elektrischen Schwingkreis z.B. aus der Induktivität L der Spule und der Kapazität C des Kondensators:

$\omega_0^2 = 1/(L\,C)\,. $

Um die Sinus-förmige Schwingung eines Oszillators zu beschreiben, werden noch weitere Begriffe verwendet, die jedoch aus den bisher vorgestellten Eigenschaften bestimmt werden können. So wird unter der Schwingungs- oder Periodendauer T die Zeit verstanden, die das System für eine vollständige Schwingung benötigt. Da sie als Informationen die Anzahl an Schwingungen und eine Zeit enthält, muss sie eng mit der Eigenfrequenz zusammenhängen: T=2\pi /\omega_0 \,.

Darstellung einer ungedämpften Schwingung

Überblick über die wichtigsten Begriffe zur Beschreibung einer Schwingung (Quelle: leifiphysik.de)

Ungedämpfter harmonischer Oszillator

Immer dann, wenn ein schwingfähiges System mit der obigen Gleichung beschrieben werden kann, handelt es sich um einen ungedämpften harmonischen Oszillator. Denn an der Gleichung wird klar, dass die Amplitude, also die maximale Auslenkung, auch bei der 20ten, 100ten, 10.000ten Schwingung wieder erreicht wird. Da sich die Systemeigenschaften ohne äußere Einflüsse ebenfalls nicht ändern, ändert sich das Verhalten dieses Oszillators nie und er schwingt stets gleich um die Ruhelage.

Nach der mathematischen Herleitung ist schon fast alles zum ungedämpften harmonischen Oszillator gesagt, denn: Reale Beispiele und Anwendungen gibt es nicht! In der Realität gibt es immer einen Widerstand, der den Oszillator ausbremst und die Auslenkung langsam kleiner werden lässt. Aus diesem Grund ist der ungedämpfte Oszillator nur zum Kennenlernen und Verstehen des Verhaltens sowie als Näherungslösung geeignet.

Gedämpfter harmonischer Oszillator

Beim gedämpften harmonischen Oszillator existiert eine bremsende Kraft. Das ändert die mathematische Beschreibung in der Differentialgleichung. Die Bewegungsgleichung des Federpendels (und äquivalent die Gleichungen anderer Oszillatoren) wird um einen Term ergänzt, der im einfachen Fall der Reibung in der Luft, also einem Reibungskoeffizienten \alpha und proportional zur Geschwindigkeit ist:

$ F=m\,x‘‘(t)=-k\,x-\alpha\,x’(t) \quad \Leftrightarrow \quad x‘‘(t)+\alpha/m\,x’(t)+\omega_0^2\,x(t)=0\,.$

Oft wird \alpha/(2m) zu \beta zusammengefasst, um das rechnen zu vereinfachen. Die zu lösende Differentialgleichung wird auf die gleiche Art gelöst, wird aber natürlich komplizierter. Als Lösungsansätze empfehlen sich wieder Sinus-, Cosinus- oder e-Funktion. Mit dem Ansatz x(t)=e^(\lambda\,t) ergeben sich Lösungen, wenn \lambda die folgende Gleichung erfüllt:

$\lambda^2+2\,\beta\,\lambda+\omega_0^2=0 \quad\Leftrightarrow \quad\lambda_{1,2}=-\beta+-\sqrt{\beta^2-\omega_0^2}\,.$

Je nachdem, wie das Verhältnis von Dämpfung und Eigenfrequenz sind, werden verschiedene Fälle unterschieden:

Schwach gedämpfter Fall

Der schwach gedämpfte Fall tritt auf, wenn \beta<omega_0 gilt. Somit ist die Zahl unter der Wurzel bei der Berechnung von \lambda_{1,2} negativ und die Wurzel selbst imaginär. Mit der verkürzten Schreibweise

$i\,\sqrt{\beta^2-\omega_0^2}=\sqrt{\omega_0^2-\beta^2}=:\omega $

ergibt sich die allgemeine Lösung zu

$x(t)=e^{-\beta\,t}\,(a_1\,e^{i\,\omega\,t}+a_2\,e^{-i\,\omega\,t}) $

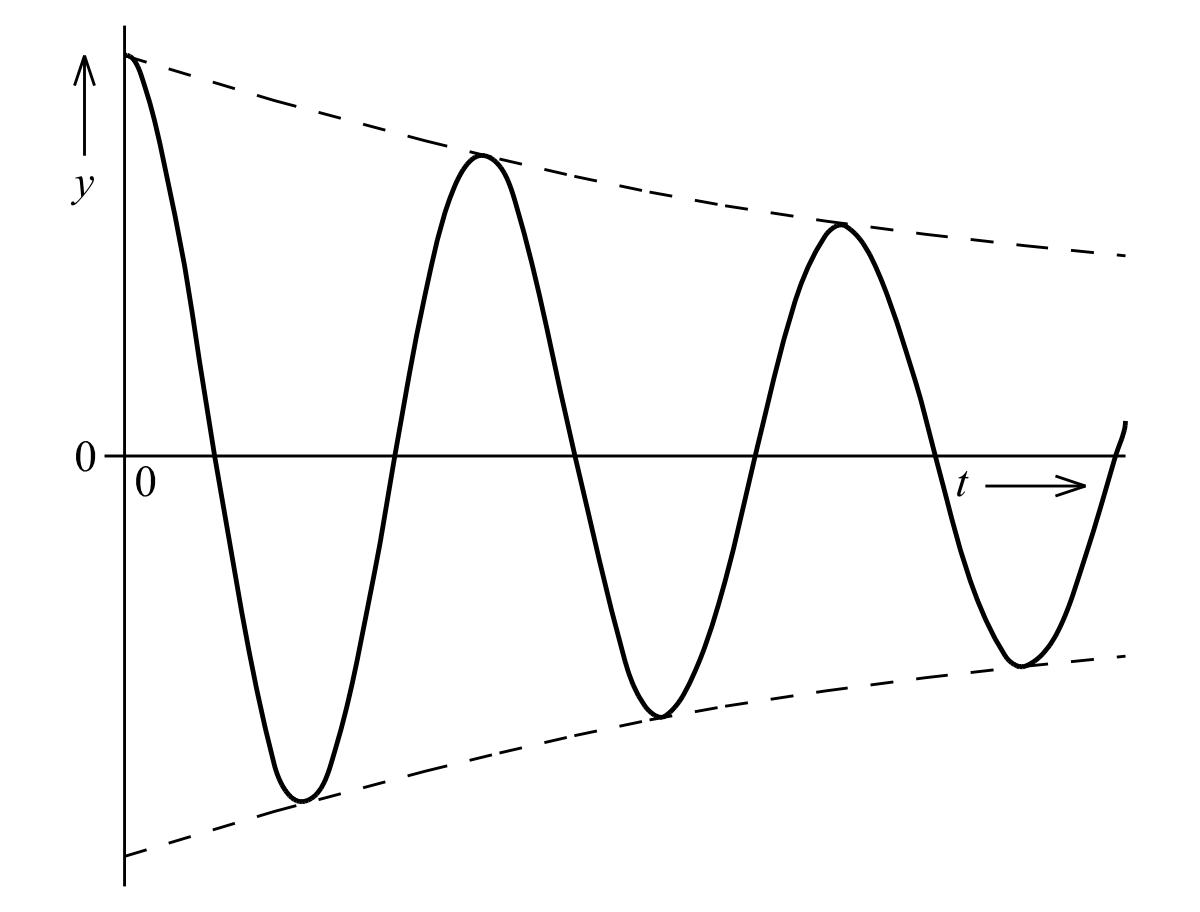
was im Vergleich mit der ungedämpften Schwingung eine Schwingung mit kleinerer Frequenz (da \omega<\omega_0) und einer mit der Zeit exponentiell abnehmenden Amplitude darstellt. Eine andere Darstellungsweise ist folgende:

$x(t)=A\,e^{-\beta\,t}\sin(\omega \, t+\phi)\,.$

Hier ist die exponentielle Abnahme der Amplitude A besser ersichtlich, allerdings ist dazu das Verständnis des Zusammenfassens zweier auftretender periodischer Funktionen mittels Phasenverschiebung \phi nötig.
Die Schwingung schwingt in diesem Fall weiterhin um die Ruhelage, allerdings wird, wie bereits gesagt, die maximale Auslenkung mit jeder Schwingung geringer.

Schwingung gedämpft.svg

Die Einhüllende zu einer gedämpften Schwingung (Quelle: Wikipedia/Harmonischer-Oszillator)

Aperiodischer Grenzfall

In Anwendungen ist es oft gewollt, eine Schwingung schnellstmöglich zu stoppen und zur Ruhelage zurückzukehren. Wenn eine Dämpfung keine komplette Fixierung in einem Zustand beinhaltet, ist eine überstarke Dämpfung dabei aber nicht zielführend, wie intuitiv oft angenommen wird. Um die Schwingung schnellstmöglich zu stoppen, ist die Bedingung \omega=0 nötig. Somit verschwindet in der Berechnung von \lambda_{1,2} die Wurzel und es bleibt nur eine Lösung übrig, was für die Schwingung zu

$x(t)=(a_1+a_2t)\,e^{-\beta\,t}$

führt, wobei a_1 und a_2 aus den Anfangsbedingungen, also Auslenkung und Startgeschwindigkeit, bestimmt werden.
Beim aperiodischen Grenzfall, manchmal auch mit kritischer Dämpfung bezeichnet, findet keine Schwingung mehr statt. Je nach Anfangsbedingungen kann die Ruhelage einmal durchlaufen werden, spätestens dann wird sich dieser allerdings exponentiell angenährt.

Aperiodischer Grenzfall.png

Darstellung des aperiodischen Grenzfalls mit unterschiedlichen Startgeschwindigkeiten (Quelle: https://de.wikipedia.org/wiki/Aperiodischer_Grenzfall)

Starke Dämpfung

Zwar führt eine starke Dämpfung auch dazu, dass keine Schwingung stattfindet, allerdings braucht das System lange, um wieder in die Ruhelage zurückzukehren. Deshalb wird dieser Fall auch als Kriechfall bezeichnet. Mathematisch wird er mit der Bedingung \beta>\omega_0
beschrieben, was zu zwei reellen, negativen Ergebnissen für \lambda_{1,2} führt. Die Bewegungsgleichung ergibt damit vereinfacht

$x(t)=e^{-\beta t}\,(a_1\,e^{\lambda t}+a_2\,e^{\lambda t})\,,$

wobei a_1 und a_2 wieder aus den Anfangsbedingungen bestimmt werden.

Vergleich des Kriechfalls mit dem aperiodischen Grenzfall
leifiphysik - Federpendel gedämpft

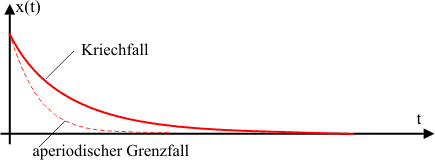
Um zu zeigen, dass die vorgestellten Fälle alle von Nutzen sind, werden nun einige Anwendungsbeispiele vorgestellt. So ist der Fall der schwachen Dämpfung für Saiteninstrumente wichtig, da die einzelnen Saiten sich nicht sofort wieder in die Ruhelage begeben dürfen, sondern schwingen müssen, um überhaupt einen Ton erzeugen zu können. Der aperiodische Grenzfall ist beispielsweise für Autofahrer sehr wichtig, da die Stoßdämpfer nach diesem Prinzip funktionieren. Das hat den einfachen Grund, dass das Auto nach der Beanspruchung der Stoßdämpfer schnell wieder in die ideale Straßenlage kommen soll. Würde eine schwache Dämpfung verwendet werden, so würde das Auto noch für längere Zeit auf und ab wippen und die Fahrt eher einer Bootstour ähneln, was wenig komfortabel ist. Bei starker Dämpfung könnte es vorkommen, dass die nächste Beanspruchung nicht ausreichend abgefedert werden kann, da die Feder noch zu stark eingefedert ist. Aber auch die starke Dämpfung hat ihre Anwendungsgebiete. So sind beispielsweise viele Türen in öffentlichen Gebäuden stark gedämpft. Das sorgt für ein langsames und leises Schließen der Türen und verhindert, dass die Tür einer unaufmerksamen Person mit zu viel Geschwindigkeit entgegenfällt und diese eventuell verletzt.

Getriebener Oszillator

Bisher wurde der Oszillator ohne äußere Kräfte betrachtet. Liegt solch eine Kraft vor, muss diese in die Bewegungsgleichung integriert werden:

$x‘‘(t)+2\beta\,x‘(t)+\omega_0^2 x(t)=1/m\,F(t)\,.$

Interessant ist dieser Fall besonders dann, wenn es sich bei der Kraft um eine periodische Kraft handelt, also F(t)=F\cos(\omega\,t). Dieser Fall ist sehr gut mit einem schaukelndem Kind zu vergleichen, welches immer zum gleichen Zeitpunkt mit der gleichen Kraft angeschubst wird.
Durch diese von außen aufgebrachte Kraft wird aus der homogenen eine inhomogene Differentialgleichung. Um diese zu lösen muss die Lösung der homogenen Differentialgleichung, welche in dem Abschnitt zu dem gedämpften harmonische Oszillator zu finden ist, mit der sogenannten partikulären Lösung addiert werden.

$x_{inh}(t)=x_{hom}(t)+x_{part}(t)$

Die partikuläre Lösung lässt sich mit dem Ansatz des Typs der rechten Seite lösen und ergibt sich zu

$x_{part}(t)=abs(A)\cos(\omega\,t+\phi)\,,$

dabei handelt es sich bei \phi um eine Phasenverschiebung zwischen der antreibenden Kraft und dem um den Ruhepunkt schwingenden Massepunkt.
Von besonderem Interesse ist dabei das Verhalten des gesamten Systems für verschiedene Frequenzen der treibenden Kraft. Dabei werden drei verschiedene Fälle betrachtet.

Niederfrequenter Bereich: f<<f_0

Für den niederfrequenten Bereich gilt, dass die Frequenz der antreibenden Kraft sehr viel kleiner ist als die Eigenfrequenz des Oszillators. Aufgrund dessen ist die Amplitude der anregenden Kraft in etwa so groß wie die Amplitude des Massepunktes. Das Amplitudenverhältnis beträgt also ungefähr 1. Der Phasenunterschied zwischen den beiden Schwingungen ist in etwa 0.

Resonanzfall: f=f_0

Von Resonanz wird gesprochen, wenn die Frequenz der antreibenden Kraft der Eigenfrequenz des Oszillators gleicht. Infolgedessen erhöht sich die Amplitude des Oszillators gegenüber der Amplitude des Erregers, sodass sich ein Amplitudenverhätnis ergibt, welches größer 1 ist. Die Phasendifferenz beträgt \phi=\pi/2, wobei der Erreger dem Massepunkt vorauseilt.

Hochfrequenter Bereich: f>>f_0

Sollte die Frequenz der antreibenden Kraft viel größer sein als die Eigenfrequenz des Oszillators so fällt auch die Amplitude des Oszillators wesentlich kleiner aus. Es ergibt sich ein Amplitudenverhätnis, welches gegen 0 geht. Auch in diesem Fall gibt es eine Phasendifferenz \phi\approx\pi, die Schwingungen laufen also fast gegenphasig ab.

Auch diese Eigenschaften der Oszillatoren sind im Alltag von Bedeutung. So ist es für Autos wichtig, dass die Eigenfrequenz einzelner Teilsysteme oder des Gesamtsystems nicht im Bereich der Motorendrehzahl liegen um eine komfortable und sichere Fahrt zu gewährleisten. Insbesondere der Resonanzfall kann gefährliche Auswirkungen haben, da in diesem Fall das System immer weiter aufgeschaukelt wird und die Amplitude des Oszillators sich immer weiter erhöht. Falls das System nicht gedämpft ist, kann die Amplitude bis ins Unedliche steigen, was zur Zerstörung des Systems führt. Eine starke Dämpfung kann die maximale Amplitude zwar begrenzen, aber auch in diesem Fall komm es für den Resonanzfall zu einer starken Belastung des Systems, was in den meisten Fällen vermieden werden sollte. Ein gutes Beispiel für eine Resonanzkatastrophe ist die Tacoma Narrows Bridge, welche durch starke Winde in Schwingung versetzt wurde, welche sich dann selbsterregt immer weiter verstärkte, was den Einbruch der Brücke zur Folge hatte.

Demgegenüber bleibt aber zu sagen, dass ohne Resonanz auch viele alltägliche Dinge nicht möglich wären, es also auch einen positiven Aspekt gibt. So würde Schaukeln nicht halb so viel Spaß machen, wenn es nicht möglich wäre seine eigene Schwingung zu verstärken und somit immer höher Schaukeln zu können. Ein weiteres typisches Beispiel für den getriebenen harmonischen Oszillator stellt der elektrische Schwingkreis da, der bei der drahtlosen Energieübertragung genutzt wird. Das System wird dabei ständig neu mit Energie aufgeladen, die es dann mittels sogenannter resonant induktiver Kopplung an einen Empfänger weitergeben kann, der so kabellos geladen wird.

Weiterführendes

Viele weiterführende Beispiele, die sich des Oszillators mit schwacher Dämpfung bedienen, sind in der Akustik respektive Musik zu finden, wie die Schwingung einer (Gitarren-)Seite, die nach einmaligem Anschlag möglichst lange klingen soll. Doch hier handelt es sich nicht um einen einfachen harmonischen Oszillator, sondern um ein komplexeres System.

Literatur und weiterführende Informationen


Podcasts

  • Helen: Schaukeln, Gespräch mit G. Thäter im Modellansatz Podcast, Folge 114, Fakultät für Mathematik, Karlsruher Institut für Technologie (KIT), 2016.