Incredible Proof Machine

In den Räumen des Entropia e.V. traf sich Joachim Breitner mit Sebastian Ritterbusch, um ihm von Computerbeweisen und der Incredible Proof Machine (http://incredible.pm/) zu erzählen. Diese hatte er mit Unterstützung von Kollegen und Freunden für einen dreitägigen Workshop im Oktober 2015 am Science College Jülich mit Schülerinnen und Schülern im Start-Stipendium für motivierte und neu zugewanderte Jugendliche in Mittel- und Oberstufe unter Unterstützung der Deutsche Telekom Stiftung entworfen.
Der mathematische Beweis ist grundlegender Bestandteil der Mathematik und die Technik des Beweisen wird im Mathematik- oder Informatikstudium vielfach geübt, wie es auch im Modell036 Podcast zur Analysis beschrieben wurde. Dennoch wird das wichtige Thema nur selten in der Schule angesprochen, da korrekte Beweise sehr formal und abstrakt sind. Mit einem spielerischen Zugang wird der Einstieg in die exakte Beweistheorie für Schüler und Mathematik-Interessierte nicht nur möglich, sondern ermöglicht auch neue Formen der Lehre wie den Modell051 Flipped Classroom.
Beweise gehen von bestehenden Aussagen und festgelegten Axiomen aus, um neue Aussagen oder Erkenntnisse zu belegen. Von der Aussage "es regnet" kann man beispielsweise mit einem fiktiven Axiom "wenn es regnet, werden Straßen nass" schließen, dass gilt: "die Straße ist nass". Und man kann daraus mit der Technik des Widerspruch-Beweis zeigen, dass aus der Aussage "die Straße ist trocken" folgt, dass "es regnet nicht" gilt. Denn (und das ist der Beweis), würde es regnen, so wäre die Straße nass, also nicht trocken.
Wann ist aber nun ein Beweis richtig? Diese Frage kann sich jeder selbst beantworten, in dem man einen vorliegenden Beweis versucht nachzuvollziehen. Eine Alternative ist die Beweisprüfung mit dem Computer, wie beispielsweise mit Isabelle. Diese Art von Software richtet sich allerdings in erster Linie an fortgeschrittene Nutzer und setzt Kentnisse in sowohl in der Logik als auch in der (funktionalen) Programmierung voraus, und so suchte Joachim nach einer einfachereren Methode, beweisen zu lernen und die Ergebnisse maschinell zu prüfen.
Mit der von ihm kreierten Incredible Proof Machine werden Beweise durch Ziehen und Setzen bildlich erstellt, in der Form eines Graphen. So wird das Beweisen zu einem Puzzle-Spiel mit Erfolgserlebnis, das man nach und nach lösen kann, ohne dabei die exakte Mathematik zu verlassen.
In dem Spiel gibt es viele Aufgaben, die zu lösen sind. In der Übersicht sind diese in Lektionen geordnet und zeigen jeweils durch einen breiten Strich, dem Inferenzstrich getrennt, von welchen Aussagen oben man welche Aussagen unten beweisen soll. Wählt man eine Aufgabe aus, so sieht man die gegebenen Aussagen, die oberhalb des Striches waren, als Quellen auf einem Arbeitsblatt. Die zu beweisenden Aussagen erscheinen als Senken. Von den Quellen kann man nun per Maus Verbindungen zu den Senken ziehen- entweder direkt, oder mit Hilfe zusätzlicher Blöcke, bzw. gegebener Beweisregeln, aus einer Toolbox links, die ebenfalls zur Verfügung stehen und weitere gegebene Axiome darstellen. Sind alle offenen Senken bewiesen, so leuchtet unten eine Zeile grün auf, als Bestätigung für einen geschafften Level- eine positive Bestärkung, die nicht ganz so spektakulär ist, wie bei Populous.
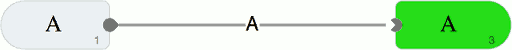
Während man auf dem Arbeitsblatt spielt, gibt die Incredible Proof Machine unmittelbar Rückmeldung, falls eine Verbindung so keinen Sinn macht: Will man die Aussage B mit Aussage A beweisen, so wird die Linie zwischen den beiden sofort rot, und gibt dem Spielenden die Hilfestellung, wo mindestens ein Fehler steckt.

Die logischen Aussagen und die gegebenen Beweisregeln verwenden eine gängige Notation zur Beschreibung logischer Verknüpfungen. Ein ∨ (sieht wie der kleine Buchstabe v aus), steht für die logische Oder-Verknüpfung und die Notation stammt vom lateinischen Wort vel. Das umgekehrte Symbol ∧ steht für die logische Und-Verknüpfung. In der ersten Lektion gibt es zwei Blöcke bzw. Beweisregeln für die Und-Verknüpfung: Einmal ein Block mit zwei Eingängen X und Y und einem Ausgang X∧Y, sowie einem Block mit einem Eingang X∧Y und zwei Ausgängen X und Y. Die Lektion 1 behandelt damit den grundlegenden Umgang mit dem System und die Konjugation.

Die Lektion 2 führt die Implikation ein. Eine Implikation, oder auch Folge, beschreibt die Aussage, dass aus einer Aussage eine zweite zwingend folgt. Zur Anwendung einer Implikation gibt es in dieser Lektion eine Beweisregel, die eine Implikation anwendet.

Ein weiterer Block ermöglicht eine Implikation zu erzeugen, in dem die Vorbedingung in einem Einschub angenommen bzw. angeboten wird, und man daraus das Zielereignis dann herleiten muss.
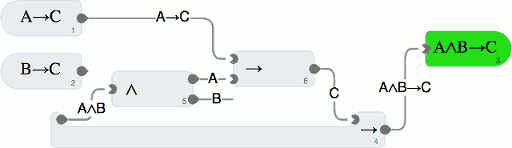
Die Prüfung der Beweise in der Incredible Proof Machine erfolgt durch einen Beweisprüfer in Haskell, einer funktionalen Programmiersprache, die auch schon im Modell047 Podcast zum Tiptoi zur Sprache kam. Der Beweisprüfer wurde mit ghcjs nach JavaScript kompiliert und läuft damit komplett im Browser. Über einen Compiler von Haskell zu Redstone wie in dem Modell056 Podcast zu Minecraft ist leider noch nichts bekannt.
Ein lehrreicher Zusammenhang ist hier, dass aus logischer Sicht Implikationen vollkommen korrekt sind, wenn die rechte Seite wahr ist – ohne dass ein ursächlicher Zusammenhang bestehen muss. Wenn also jemand nach Einnahme von offensichtlich unwirksamen Mitteln gesund geworden ist, so ist der logische Schluss, dass nach der Einnahme die Person gesund ist, korrekt. Doch darf man daraus keinesfalls schließen, dass die unwirksamen Mittel dafür der Grund gewesen wären. Das ist ein ähnlicher Fehlschluss wie Cum hoc ergo propter hoc – aus Korrelation folgt keine Kausalität.
Die Lektion 3 führt die Disjunktion bzw. Oder-Verknüpfung mit drei neuen Beweisregeln-Blöcken ein, zwei zur Erzeugung einer Aussage mit einer Disjunktion, eine zur Zerlegung einer Disjunktion. Interessant ist dabei besonders die Zerlegung der Disjunktion, da sie auf eine Fallunterscheidung führt.

Man kann auch frei weitere Aufgaben innerhalb der Incredible Proof Machine für sich selbst hinzufügen, neue Vorschläge aber auch auf Github einreichen.
Die Lektion 4 behandelt die abstrakte falsche Aussage ⊥. Aus dieser kann man alles folgern, ex falso quodlibet, was dann auch in der ersten Aufgabe zu zeigen ist. Eine besondere Notation ist dabei, dass aus einer Aussage falsch folgt, wie A→⊥. Dies bedeutet einfach nur, dass A nicht gilt, also falsch ist – die Negation von A.
In Lektion 5 verlassen wir dann die intuitionistische Logik, die von einer konstruktiven Mathematik ausgeht, hinein in die allgemeinere klassische Logik. Hier wird die Beweisregel vom ausgeschlossenen Dritten (tertium non datur) eingeführt. Dabei sind konstruktive Beweise, die also ohne tertium non datur auskommen, leichter automatisiert zu führen.
Für die Aussage "Es gibt eine irrationale Zahl, die mit einer irrationalen Zahl potenziert rational ist" gibt es als Beispiel einen nicht-konstruktiven Beweis: Entweder ist Quadratwurzel von 2 mit sich selbst potenziert rational, oder spätestens das Ergebnis potenziert mit der Quadratwurzel von zwei ist rational, denn das ist 2. Es ist nicht klar, welche Basis die Lösung ist, sondern hier nur, dass es eine der beiden ist.
Einen Zusammenhang von der konstruktiven Logik zur Programmierung liefert die Theorie der Curry-Howard-Korrespondenz – man kann Programmieren auch als eine Art Beweisen sehen, und daher sind auch ähnliche graphische Darstellungen als Flussdiagramm möglich.
In Lektion 6 werden Quantoren und Prädikate eingeführt. Man kann hier beispielsweise zeigen, wann der Existenzquantor und der Allquantor vertauscht werden dürfen:

Die Lektion 7 behandelt zwei weitergehende Beispiele, die auch umgangssprachlich verständlich sind: Die erste Aufgabe behandelt das Bar-Paradox: Hier gilt es zu beweisen, dass es in jeder nicht-leeren Bar immer eine Person gibt, dass wenn sie trinkt, alle in der Bar trinken. Die zweite Aussage lautet: Wenn jeder Mann einen reichen Vater hat, dann gibt es einen reichen Mann mit einem reichen Großvater.

Die klassische Aussagenlogik kann aber auch über andere Kalküle definiert werden: So demonstriert die Incredible Proof Machine die Verwendung des Hilbert-Kalküls und das NAND-Kalküls. Während das Hilbert-Kalkül besonders theoretisch verwendet wird, liefert das NAND-Gatter als einfacher Logikbaustein Anwendungen bis hin zum Volladierer aus NAND-Gattern.
Man kann auch jederzeit neue Beweisregeln oder Lemmas definieren, in dem man alle Bausteine logischer Diagramme mit offenen Ein- und Ausgängen mit gedrückter Shift-Taste anwählt und links zu einem neuen Baustein zusammenführt. Das folgende Bild zeigt die Definition des Beweis durch Widerspruch, und die anschließende Verwendung zu Lösung einer Aufgabe in Lektion 5:
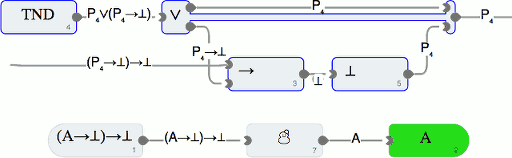
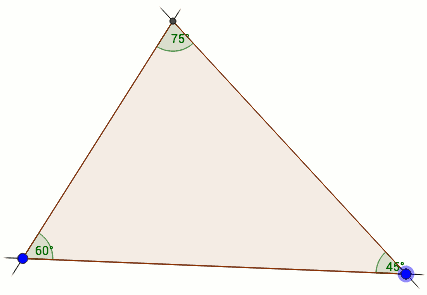
Im Gegensatz zur Incredible Proof Machine soll die Software Isabelle nicht vom Nutzer verlangen, alle Beweise selbst zu führen, sondern unterstützt dabei, Beweise auf einem hohen Abstraktionsgrad zu formulieren und zu beweisen. Ein kleines Beispiel für die Nutzung von Isabelle ist der humorvolle Versuch das allgemeine Dreieck zu definieren – und letzlich die eindeutige Existenz zu beweisen.
Eine wichtige Anwendungen für Computerbeweise ist die formale Prüfung und der Beweis von Computersoftware, wie sie beispielsweise durch die Launchbury Semantik möglich wird. Sehr bekannt ist die Nutzung von rechnerunterstützten Beweisen für das Vier-Farben-Problem, das Hermann Minkowski in einer Topologie-Anfängervorlesung vergeblich versuchte nebenbei zu lösen. Der erste Beweis war noch sehr umstritten, da die Korrektheit der verwendeten Software nicht gesichert war. Erst mit einer formalen Prüfung in Coq wurde der Beweis 2005 allgemein akzeptiert.
Eine andere gängige Methode ist auch die Verwendung spezialisierter Verifikationsnumerik, um die Existenz von Lösungen zu beweisen, wie dies auch im Modell019 Podcast zum computerunterstützten Beweisen behandelt wird.
Auch die dichteste Kugelpackung, bzw. die Keplersche Vermutung, wurde erst 1998 mit Computerhilfe bewiesen, der zunächst ebenso umstritten war. Erst mit dem Projekt Flyspec konnte 2014 die Korrektheit des Beweises formal bewiesen werden.
Im Hintergrund der Aufnahme hört man den Freifunk Karlsruhe, der parallel zu unserem Gespräch ein Treffen in den Räumen des Entropia e.V. hatte. Kinder und Jugendliche, die sich für Programmieren interessieren, sollten sich ein CoderDojo, wie das CoderDojo in Karlsruhe, genauer ansehen.
Literatur und Zusatzinformationen
- Einführender Blog-Eintrag zur Incredible Proof Machine mit einer Sammlung von ähnlichen Projekten.
- J. Breitner: The Correctness of Launchbury's Natural Semantics for Lazy Evaluation, arXiv preprint arXiv:1405.3099, 2014.
- J. Breitner: The Safety of Call Arity, Archive of Formal Proofs, 2015.
- J. Breitner: Formally Proving a Compiler Transformation Safe, Haskell '15 Proceedings of the 2015 ACM SIGPLAN Symposium on Haskell, Pages 35-46, ACM New York, NY, USA, 2015.
- T. Nipkow, L. Paulson, M. Wenzel: Isabelle HOL- A Proof Assistant for Higher-Order Logic, Springer-Verlag, 2015.
Podcasts
- T. Schwentick: Logik, Gespräch mit N. Ludewig im Omega Tau Podcast, Folge 101, Omega Tau, 2012. http://omegataupodcast.net/2012/08/101-logik/
- D. Rütters: Computerunterstütztes Beweisen, Gespräch mit G. Thäter im Modellansatz Podcast, Folge 19, Fakultät für Mathematik, Karlsruher Institut für Technologie (KIT), 2014. http://modellansatz.de/beweisen
- J. Eilinghoff: Analysis, Gespräch mit S. Ritterbusch im Modellansatz Podcast, Folge 36, Fakultät für Mathematik, Karlsruher Institut für Technologie (KIT), 2014. http://modellansatz.de/analysis
- J. Breitner: Papierrechner, Gespräch mit S. Ritterbusch im Modellansatz Podcast, Folge 47, Fakultät für Mathematik, Karlsruher Institut für Technologie (KIT), 2015. http://modellansatz.de/papierrechner
- C. Spannagel: Flipped Classroom, Gespräch mit S. Ritterbusch im Modellansatz Podcast, Folge 51, Fakultät für Mathematik, Karlsruher Institut für Technologie (KIT), 2015. http://modellansatz.de/flipped-classroom
- F. Gilges: Spielcomputer, Gespräch mit S. Ritterbusch im Modellansatz Podcast, Folge 56, Fakultät für Mathematik, Karlsruher Institut für Technologie (KIT), 2015. http://modellansatz.de/spielcomputer